Binary, Bits, and Bytes

Binary numbers are the cornerstone of digital computing, serving as the fundamental language of modern computers.

Binary Numbers

Unlike the base-10 decimal system that is commonly used, which relies on 10 digits (0 through 9), binary operates with just two digits: 0 and 1. This simplicity makes it ideal for representing and manipulating data in electronic circuits, where signals are either “on” (1) or “off” (0).

The animation below demonstrates the 256 possible combinations with eight light switches .

Binary numbers work on the principle of representing numbers using only two digits: 0 and 1. In the binary system, each digit’s position represents a power of 2, starting from the rightmost digit, which represents:

• $2^0=1$

• $2^1=2$

• $2^2=4$

• $2^3=8$

• $2^4=16$

• $2^5=32$

• $2^6=64$

• $2^7=128$

Here are the binary numbers and there base-10 equivalents from 0 - 99:

Note

It is common to represent binary numbers with a subscript 2 with or without parentheses to help distinguish them from base-10 numbers. $(1001)_2 = 9$ or $1001_2 = 9$

0 - 9	10 - 19	20 - 29	30 - 39	40 - 49	50 - 59	60 - 69	70 - 79	80 - 89	90 - 99
0	1010	10100	11110	101000	110010	111100	1000110	1010000	1011010
1	1011	10101	11111	101001	110011	111101	1000111	1010001	1011011
10	1100	10110	100000	101010	110100	111110	1001000	1010010	1011100
11	1101	10111	100001	101011	110101	111111	1001001	1010011	1011101
100	1110	11000	100010	101100	110110	1000000	1001010	1010100	1011110
101	1111	11001	100011	101101	110111	1000001	1001011	1010101	1011111
110	10000	11010	100100	101110	111000	1000010	1001100	1010110	1100000
111	10001	11011	100101	101111	111001	1000011	1001101	1010111	1100001
1000	10010	11100	100110	110000	111010	1000100	1001110	1011000	1100010
1001	10011	11101	100111	110001	111011	1000101	1001111	1011001	1100011

Bits and Bytes

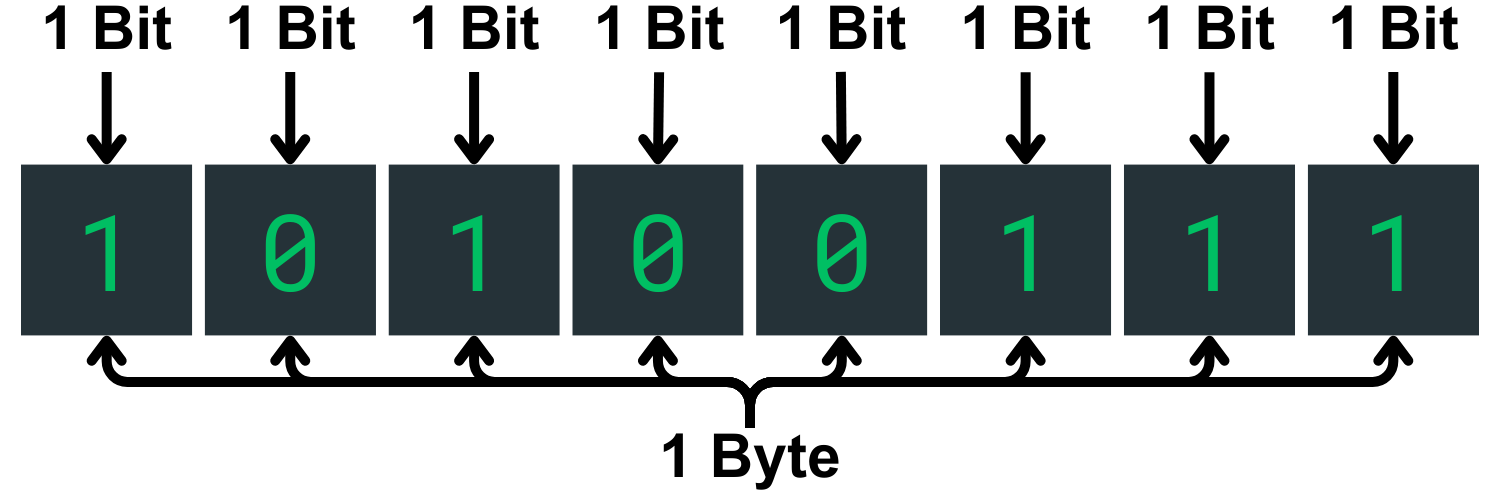
TODO

Binary Expansion

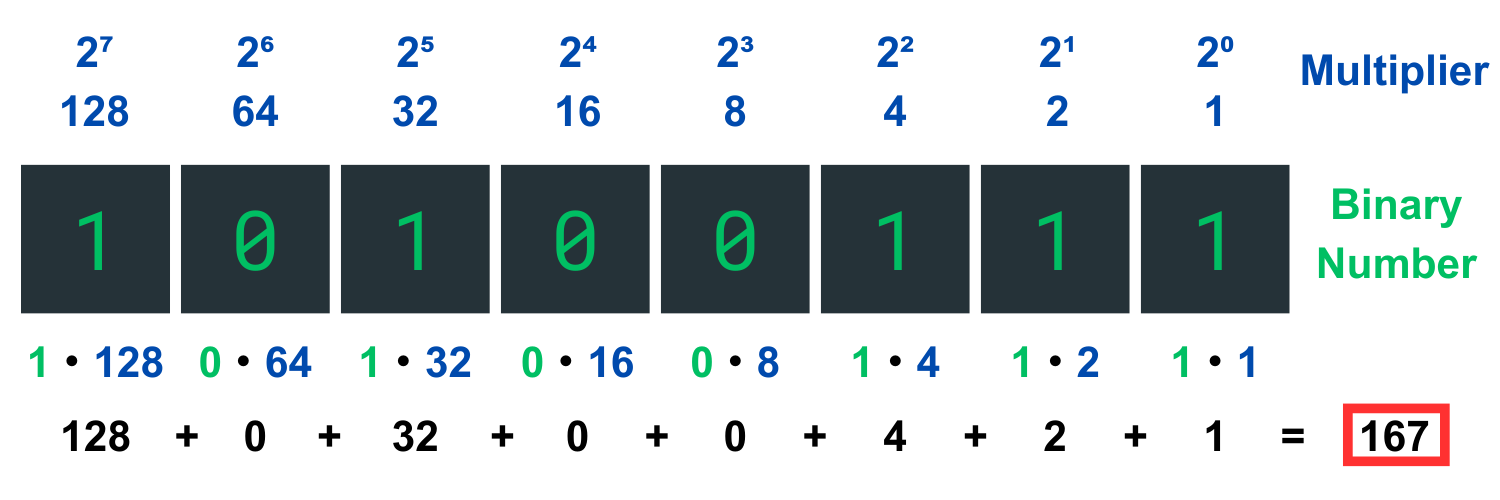
$$ \begin{align} (1010 \space 0111)_2 &= 1 \cdot 2^7 + 0 \cdot 2^6 + 1 \cdot 2^5 + 0 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 1^0 \ &= 1 \cdot 128 + 0 \cdot 64 + 1 \cdot 32 + 0 \cdot 12 + 0 \cdot 8 + 1 \cdot 4 + 1 \cdot 2 + 1 \cdot 1 \ &= 128 + 0 + 32 + 0 + 0 + 4 + 2 +1 \ &= 167 \end{align} $$

Checkpoint: Binary Expansion

Calculate the binary expansion of the following byte:

Click here to reveal the solutions.

Solution:

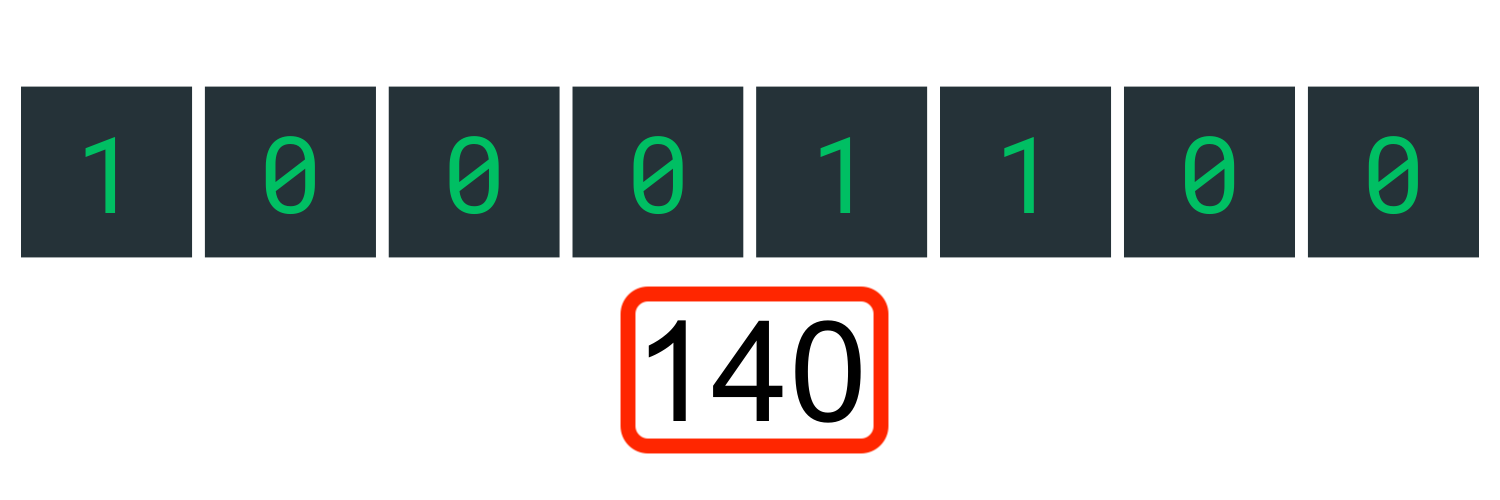
$$ \begin{align} (1000 \space 1100)_2 &= 1 \cdot 2^7 + 0 \cdot 2^6 + 0 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 0 \cdot 1^0 \ &= 1 \cdot 128 + 0\cdot 64 + 0 \cdot 32 + 0 \cdot 12 + 1 \cdot 8 + 1 \cdot 4 + 0 \cdot 2 + 0 \cdot 1 \ &= 128 + 0 + 0 + 0 + 8 + 4 + 0 + 0 \ &= 140\end{align} $$